Matrices and Determinants in Excel

Spreadsheets are excellent tools for understanding arrays. While arrays can be multi-dimensional in theory, it’s easiest to visualize them in terms of rows and columns, forming one or two-dimensional arrays.

One-dimensional Array

1. If we have the range A1:A10 with values in it, it can be treated as a 1×10 dimensional array (or a one dimensional vertical array).
2. If we have the range A1:J1 with values in it, it can be treated as a 10×1 dimensional array (or a one dimensional horizontal array)

Two-Dimensional Array

1. If we have the range A1:C5 filled with values, it can be treated as a 5×3 two dimensional array.

Arrays are always represented as rows x columns. And in many problems, it is useful to manipulate an entire array. Such an array is called a matrix (even though in Excel, the terms, “range”, “array” and “matrix” are virtually interchangeable).

Types of Matrices

1. Vectors: One dimensional matrices
2. Square Matrix: Equal number of rows and columns
3. Diagonal Matrix: Square matrix with all values except the diagonal are 0.
4. Unit Matrix: Diagonal Matrix, except the diagonal is 1. The determinant of this matrix is 1.
5. Upper Triangular Matrix: Everything below the diagonal is 0.
6. Lower Triangular Matrix: Everything above the diagonal is 0.
7. Symmetric Matrix: Square matrix with a_ij = a_ji

Determinant

A determinant is a mathematical value that can be calculated for a square matrix. They’re useful in determining solution of systems of simultaneous equations. Evaluating determinants in Excel is easily achieved using the formula =MDETERM(array).

For example, consider the following square matrix.

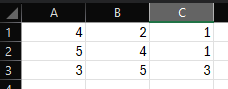
To calculate the determinant, simply type =MDETERM(A1:C3) in a cell outside the matrix to yield a value of 17.

Excel’s Built-In Matrix Functions

Excel has practically all the built in matrix functions that one would need for matrix manipulations. We’ve already seen one: MDETERM(array) which can be used to find the determinant of a square matrix. A good practice when treating an array like a matrix is to rename the array with the name of the matrix. This is achieved by simply highlighting the matrix and entering the desired name in the top left corner above the sheet.

Here are a few more:

1. Unit Matrix: The function =MUNIT(size) generates an identity matrix of a specified size. For example, =MUNIT(3) returns {1, 0, 0; 0, 1, 0; 0, 0, 1}.
2. Inverse of a Matrix: This is achieved by the formula =MINVERSE(array). An inverse of a matrix multiplied by itself results in a unit matrix.
3. Matrix Multiplication: This is achieved by the formula =MMULT(matrix1, matrix2). Matrix multiplication is possible only if the matrices being multiplied are conformable (the number of columns of the first matrix is equal to the number of rows of the second matrix).
4. Matrix Addition/Subtraction: Matrix addition/subtraction is a scalar operation. Once a matrix has been named, one can simply add the number to it. For example, =A + 2 will add 2 to each of the elements. If there were another matrix B with the same dimensions as A then =A + B would add each element in its corresponding location.
5. Scalar Multiplication/Division: For scalar multiplication or division, just use the formula =A * 2 or =A / 2 if the goal is to multiply or divide by two. You cannot do scalar multiplication/division of two matrices.
6. Transpose: The function =TRANSPOSE(array) transposes the rows and columns of a matrix. Once can manually do it by using Paste Special > Transpose.

CONCLUSION

Arrays and matrices are fundamental concepts in both mathematics and programming, and Excel provides a powerful platform to explore and manipulate these structures. From understanding basic one-dimensional and two-dimensional arrays to performing complex matrix operations, Excel’s built-in functions make these tasks straightforward and efficient.

By leveraging functions like MDETERM, MUNIT, MINVERSE, MMULT, and TRANSPOSE, you can perform a wide range of matrix manipulations directly within Excel. Whether you’re calculating determinants, generating identity matrices, finding inverses, performing matrix multiplication, or transposing matrices, Excel has you covered.

Naming your arrays for better clarity and organization, as well as understanding the different types of matrices and their properties, will further enhance your ability to work with data in a structured and efficient manner.

As you continue to explore and utilize these tools, you’ll find that Excel is not just a spreadsheet application but a robust computational tool capable of handling a variety of mathematical and logical operations.