Number Series in Excel

Number series are important in many areas of mathematics (which in turn forms the backbone of various other fields, such as Physics and Engineering) for the evaluation of transcendental functions, integrals and differential equations. More often than not, the sum of a series represents an approximation of the function. For example, the value of the base of natural logarithms, e, can be represented as:

$$e=1+\sum _{k=1}^{\infty }\frac{1}{k!}$$

Of course, Excel already provides worksheet functions to evaluate e, sin x or cos x, but the ability to create complex functions enables us to add functionality to Excel and aids us in evaluation various Number Series.

Example 1: TAYLOR SERIES

The Taylor Series is used frequently to evaluate a function by numerical methods. Given f(x), f'(x), f”(x)… etc., the Taylor series can be used to evaluate f(x+h).

The more the terms, the lower the error. Additionally, greater the value of h, the more higher order terms are desirable; and accuracy increases as h decreases.

Take for instance the equation:

We’re asked to find f(x) at x = 1.65. Obviously, this is an exact function, it is easy to calculate the value of f(x = 1.65) but for illustrative purposes, we can use this example.

The derivatives of this function are:

To set up a Taylor Series approximation in Excel, do the following:

1. Designate A1 as x and B1 as f(x).
2. In A2 enter 1. In A3 1.65. Calculate f(x) in B2 and B3 using the f(x) formula. In this example, we already know the exact formula, but often times, we may not know what the function is – and are only reliant on the value of the function and derivatives of the function at a particular point.
3. B2 should yield 0 and B3 should yield 4.337125.
4. In C6, enter ORDER, D6 enter f^k(x), E6 enter f(x+0.65) and in F6 enter Error.
5. In C7:C10 enter 1, 2, and 3.
6. In D7:D10 calculate f^k(x) based on the formulae provided above.
7. In E7, enter the following: =B2+0.65*D7
8. In E8, enter =E7+((0.65^2)/2)*D8
9. In E9, enter =E8+((0.65^3)/6)*D9
10. In F7:F10 calculate the difference between the exact result (obtained in B3) and the Taylor Series approximation obtained in E7:E10.

Your spreadsheet should look like this:

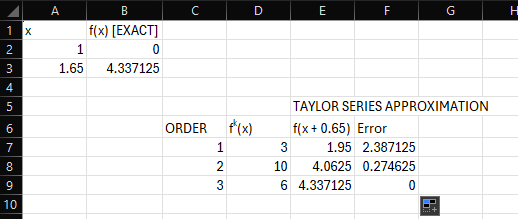
As you can see, by the time we get to the third order approximation, the Taylor Series yields an exact value.

How do you think things would change if the initial x were different? What would happen if x = 1.25 and h = 0.4?

Example 2: Heron’s Method for finding the square root of a number

The Heron’s method to calculate the square root of a number is surprisingly straightforward (and I often wish I had known this method in middle school). To find the square root of a number, n:

1. Take an initial guess, i > 0.
2. Divide the number, n, by i.
3. Take the average of i and n/i.
4. Go back to step 2 and repeat.

I have found that using i = n/2 as the initial guess works pretty well in most cases.

Here’s a VBA code to implement it:

Function Heron(n As Double) As Double

    If n < 0 Then
        Heron = Err.Number
        Exit Function
    End If
    
    Dim i As Double, e As Double
    
    i = n / 2
    e = 0.000001
    
    Do While Abs(i * i - n) > e
        i = (i + n / i) / 2
    Loop
    
    Heron = i
    
End Function

Here, the loop repeats until we get within 0.000001 of the square root of the number. To use this function, for instance to determine the square root of 13, simply type =Heron(13) in a cell on the spreadsheet. The method is surprisingly efficient and even with large numbers, we can get close to the desired results in less than 50 iterations. Take a look at the example below:

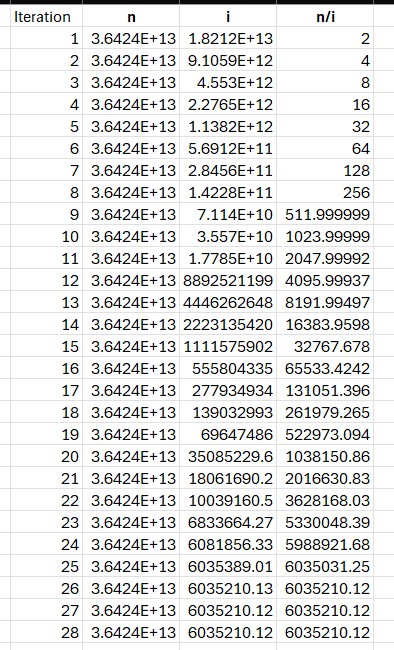
Conclusion

In this blog post, we’ve explored the significance of number series in mathematics and their applications in various fields. Using Excel, we’ve demonstrated how to implement complex mathematical concepts like the Taylor Series and Heron’s Method, highlighting Excel’s power beyond simple spreadsheets. By creating custom functions and using built-in tools, we can extend Excel’s functionality to tackle more advanced mathematical problems. Whether you’re calculating approximations of transcendental functions or finding square roots with high precision, Excel provides a versatile platform for enhancing your computational toolkit. Keep experimenting with these techniques to uncover the full potential of Excel in solving mathematical challenges. Try finding out more about other number series such as the Wallis’ series or the Machin series.